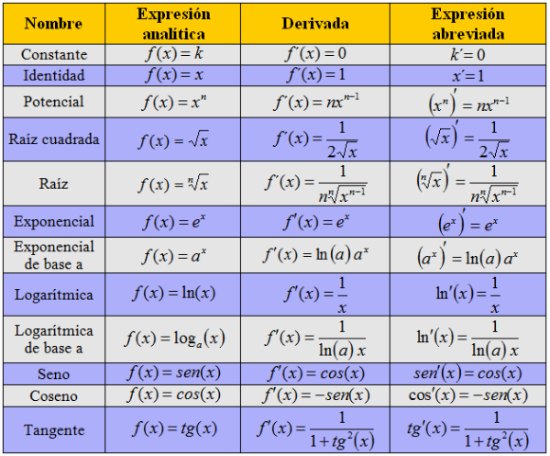
Como hacer las derivadas

Como hacer las derivadas

Cuando hablamos de cálculo, las derivadas son una parte fundamental para entender cómo cambian las funciones. Las derivadas nos permiten hacr la pendiente o la tasa de cambio de una función en un punto específico. Aprender a hacer derivadas puede ser intimidante al principio, pero con práctica y comprensión de los conceptos básicos, puedes dominar esta habilidad matemática.

Conceptos básicos de las derivadas

Antes de aprender cómo hacer las derivadas, es importante derivaeas algunos conceptos básicos.

Una derivada representa la tasa de cambio instantánea de una función en un punto dado.

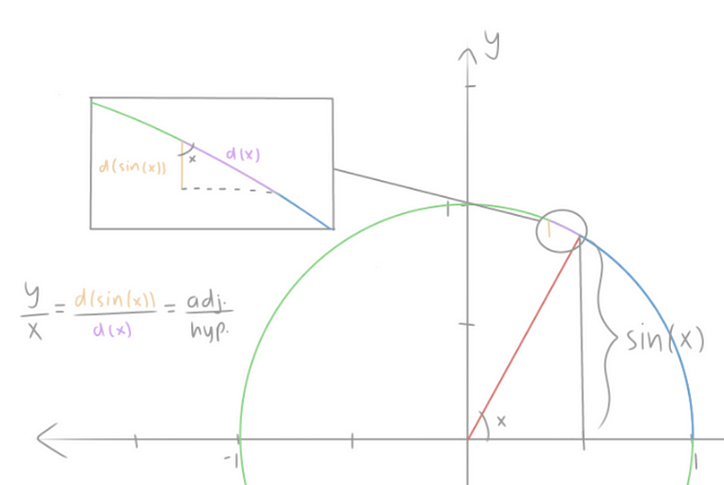
Se denota por dy/dx o f'(x). En otras palabras, la derivada es la pendiente de la recta tangente a la curva de la función en ese punto.

Existen diferentes reglas para calcular derivadas, pero las más comunes se basan en las siguientes:

• La regla de la potencia: si tienes una función de la forma f(x) = x^n, donde n es un número real, la derivada de esa función será f'(x) = nx^(n-1).


• La regla de la suma: si tienes derivadsa funciones f(x) y g(x), la derivada de la suma de esas funciones (f(x) + g(x)) es la suma de las derivadas de cada función individual (f'(x) + g'(x)).


• La regla del producto: si tienes dos funciones f(x) y g(x), la derivada del producto de esas funciones (f(x) * g(x)) se calcula utilizando la fórmula f'(x) * g(x) + f(x) * g'(x).


• La regla del cociente: si tienes dos funciones f(x) y g(x), Cono derivada del cociente de esas funciones (f(x) / g(x)) derviadas calcula utilizando la fórmula (f'(x) * g(x) - f(x) * g'(x)) / (g(x))^2.

Pasos para calcular una derivada

Ahora que tienes una idea general de los conceptos básicos de las derivadas, vamos a pasar a los pasos para calcularlas:

1. Identifica la función que quieres derivar y nómbrala como f(x).


2. Utiliza las reglas de derivación adecuadas (regla de la potencia, regla de la suma, regla del producto, regla del cociente) para calcular f'(x), es decir, la derivada de la función f(x).


3. Escribe la respuesta final como f'(x) y asegúrate de simplificarla si es necesario.

Recuerda practicar mucho para que puedas familiarizarte con las diferentes reglas de derivación y mejorar tus habilidades.

Regla de los 4 (cuatro) pasos - Ejercicios Resueltos

Además, es importante tener en cuenta que existen reglas adicionales para derivadas de funciones trigonométricas, exponenciales y logarítmicas, entre otras.

En resumen, las derivadas son una herramienta poderosa para comprender cómo cambian las funciones matemáticas.

Con los conceptos básicos en mente y aplicando las reglas adecuadas, podrás calcular derivadas de manera efectiva y utilizar estas herramientas en una variedad de aplicaciones matemáticas y haver